In my first post, I promised “a short technical note” on how the design of an astronomical clock is affected by the latitude for which it is designed. That note has refused to stay short, and so this is the first of a two-part explanation. I realise that I still haven’t written anything that simply describes the overall look of the Prague astronomical clock, and some of you might not have it on instant recall in your memory. I considered first writing a descriptive post, but I keep encountering chicken-and-egg type issues between that post and this one. In the end, since today is the solstice, I decided to go ahead with this. I can only ask that you take some information on faith until I can write more to explain it more fully.
The reason a clock designed for 50 degrees north latitude is different than a clock for any other latitude has to do with the variable length of days and nights over the course of the year. At every location on Earth except at the equator, days are longer in the summer and shorter in the winter. This difference gets more extreme as one travels away from the equator. That is how things like this can happen:

This image was taken within five minutes of local solar midnight on the summer solstice near Isafjörður, Iceland. The Sun had set, but we were so far north that the Sun was less than one degree below the horizon. We were basically at the Arctic Circle, the line of latitude above which, because of the tilt of the Earth’s axis, the Sun does not set for at least part of the year, meaning that daytime makes up 24 hours of each day. The season of midnight sun gets longer as one continues to travel north (or south). At the North (or South) Pole, the Sun rises once per year on the Spring equinox and sets once per year on the Fall equinox.
The face of the Prague astronomical clock contains a great number of arced lines and circles. I will try to explain all of these eventually, but for now, I can at least give you an image to refer to. My thanks to Jana Gluchman at praguejourneys.com for making the image available.

For this post, we are concerned with the line that divides the blue field on the upper part of the face from the red and black below. This line represents the horizon. As the hour hand of the clock travels around the dial, the figure of the Sun attached to it crosses this line twice per day. When the Sun is above the horizon line, it is daytime; when it crosses below this line, it is nighttime. The red area represents twilight, when the Sun is below the horizon but still illuminates the sky, and the black circle represents full night. The distinction is labeled on the clock face in a series of Latin words: aurora (dawn), ortus(sunrise), occasum (sunset), and crepuscus (dusk). Sunrise and sunset mark the points where the Sun crosses the horizon; dawn and dusk are defined, astronomically, as the point when the Sun is eighteen degrees below the horizon.
The image of the Sun is not simply fixed to the hour hand of the clock, which points to the various hours of the day around the edge of the clock. (There are three different ways to count the hours, represented by three different sets of numbers. Again, this is material for another post.) Over the course of the year, the Sun moves along the arm of the hour hand, approaching the center of the clock during the winter and the edge of the clock face in the summer. On the equinoxes, the Sun travels along the gold band that runs halfway out from the dial to the edge of the face. I will call this the “equinox line” or the “line of the equinox.” It is the line on which the entire clock design is based. Two other gold bands run concentric to this: one sits directly around the schematic image of the globe, the other along the edge of the clock face. On the winter solstice, the image of the Sun runs just outside the innermost band. On the summer solstice, the Sun runs just inside the outermost band.

The horizon line on the Prague astronomical clock is designed in such a way that, as the Sun moves along the arm of the hour hand, it crosses the horizon at different times of the day over the course of the year. In the fall and winter, when it is close to the center of the clock, it spends more time below the horizon line than above it. In the spring and summer, when it is in the outer reaches of the clock face, it spends more time above the horizon than below.
Here’s a simple visual test. First strip the clock face down to the concentric circles. These would be identical for any clock made for any latitude (as I will explain in part 2 of this post.) Now, run a horizontal line across the center of the clock, like this:

In this arrangement, the solstice and equinox circles—and indeed any circle centered on the center of the clock—is half above and half below the horizontal line. That means that, if this were the horizon line on the clock, then every single day and every single night of the year would be twelve hours long. Now compare this to the curved horizon line on the actual clock:

Notice that, inside the circle of the equinox, the horizon line is above the horizontal, so less than half of the circle is in the blue field, indicating that days are shorter than twelve hours, and the Sun passes through a relatively narrow band of red before and after each long night. (The Sun is never closer to the center of the clock than the inner gold band, so it will always be in the red or black.)
Outside the circle of the equinox, the horizon line is below the horizontal on both sides of the clock. This means that any circle drawn outside the equinoctial circle falls more in the day than night portion of the clock. Around the summer solstice, the Sun passes near the very edge of the clock face and completely misses the black circle of night. This represents the short nights of June in northern latitudes, the “white nights” as they are called in St. Petersburg, which sits another ten degrees north of Prague and only about six degrees south of the Arctic Circle.
We can now begin to imagine what the horizon line—the line between blue and red fields—would look like on clocks made for different latitudes. At the equator, where day and night are always of equal length, the horizon would be represented by that straight horizontal line we imagined running through the center of the clock. At the North Pole, where the Sun rises and sets once per year on the equinoxes, the horizon line would be a circle identical to the gold equinox line. On such a clock (we might call it Santa’s Astronomical Clock), as the Sun moves along the hour arm, it would pass outside the horizon line at the spring equinox, and it would stay out there for half a year, falling back below it on the fall equinox, the start of six months of darkness.

So, we might imagine an animation of how the horizon line of an astronomical clock would change as it moves north. It would begin with a flat line and then bulge upwards, the sides bending down towards one another. Eventually, they would form a circle, which would gradually rise up the clock face until it was identical to the circle of the equinox. In fact, the horizon line is always a circle, it just expands beyond the edges of the clock face for most latitudes. (The straight horizontal line representing the horizon on an equatorial astronomical clock is really just part of an infinitely large circle.)
The images above show what the horizon line would look like on clocks built for the equator (such as one at Quito or Kampala), 30 degrees (Cairo or Durban, South Africa), sixty degrees (St. Petersburg or the South Orkneys), and the North or South Pole. The horizon line for the Prague clock, designed for 50 degrees, falls between the second and third of these. If we stack all of these lines up, one important fact about these horizon lines becomes immediately evident:
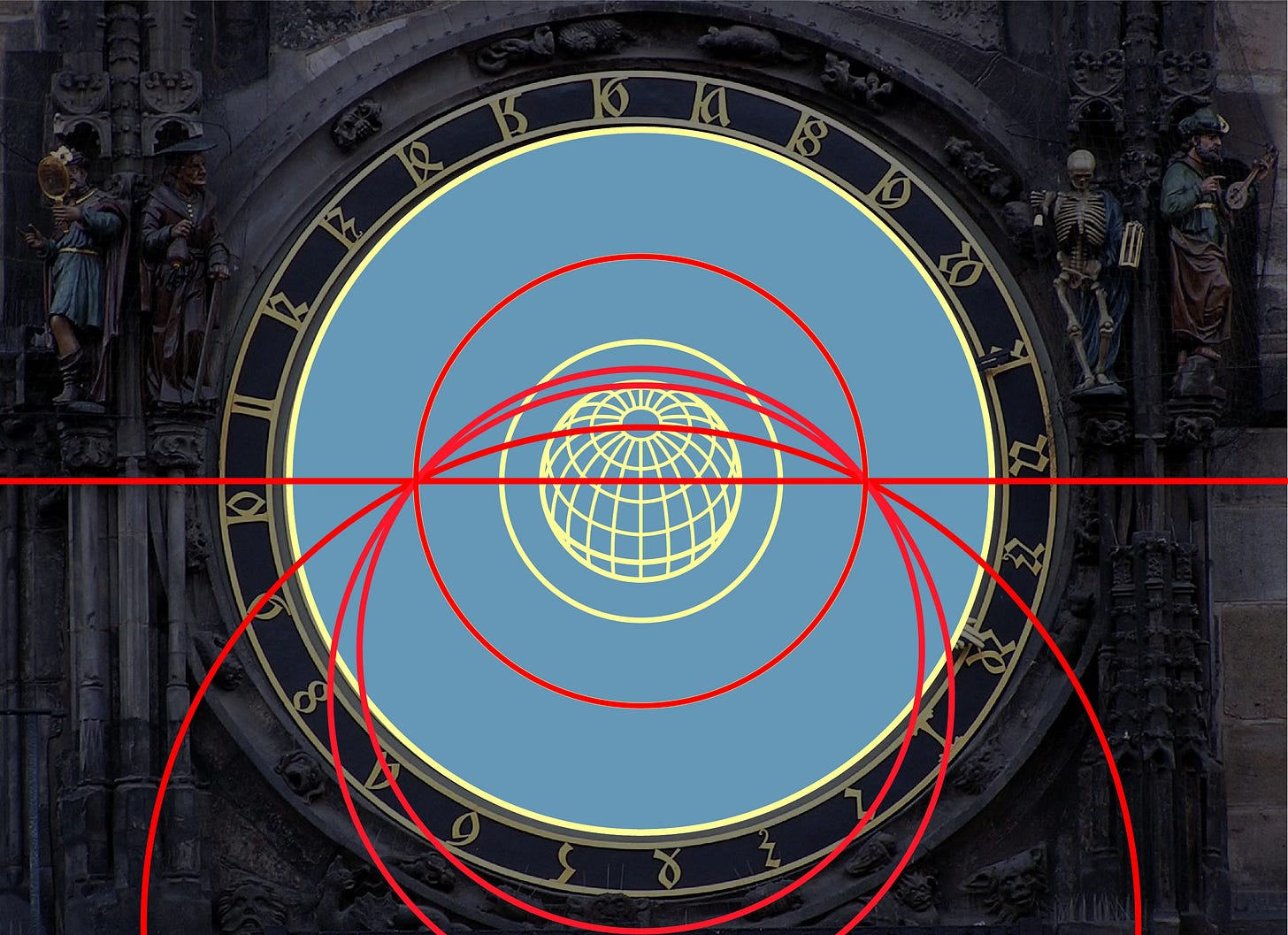
Since day and night are the same length everywhere on Earth on the spring and fall equinoxes, the horizon line of any astronomical clock anywhere will pass through the point where the horizontal line crosses the circle of the equinox, so that half of the Sun’s path that day is above the horizon, and half is below it.
We now have the basic idea of why an astronomical clock is tailored to a specific latitude: taken much to the north or south, it would still tell time, but it would not properly indicate sunrise and sunset except at the equinoxes. There remains only to demonstrate how to derive the specific shape of the horizon arc for a given latitude. That will come in a follow-up post to this one, which will be about 20% history and 80% geometry. If you don’t care about the math money shot, then you can probably ignore it. If you want to see how I came up with all the red circles in this post, then stay tuned.



